Por Bertrand Lemennicier
[Este artigo, traduzido por Vitor Gomes Calado, faz parte do livro “O Mito da Defesa Nacional”, o livro está disponível para download na página “Livros” deste mesmo site e disponível para venda aqui.]
O problema da proliferação nuclear é um problema velho, datado desde a primeira ofensiva de detonação nuclear em 1945, quando os Estados Unidos usaram armas nucleares no Japão. O problema ressurge sempre que uma nova nação desenvolve armas nucleares: a União Soviética em 1949, o Reino Unido em 1952, a França em 1962, a China e a Índia em 1974. Israel reivindica ter armas nucleares; o Brasil, África do Sul e a Argentina provavelmente também poderiam ter armas nucleares, mas pararam de desenvolvê-las; o Irã, Iraque e provavelmente outros (e.g., a Coreia do Norte) expressaram o desejo de ter armas nucleares.
Caso as armas nucleares, nas mãos dos governos, representem uma aparente ou real ameaça de intrusão ou invasão a seus vizinhos, podemos esperar movimentos por parte de nações menores para defender seu território e sua independência política através da aquisição ou produção de armas nucleares. O Governo Francês se utilizou desse argumento contra o programa nuclear dos Estados Unidos quando Charles de Gaulle subiu ao poder em 1945. Ao mesmo tempo, mudanças tecnológicas e políticas reduziram o custo da aquisição de armas nucleares. Ademais, o progresso tecnológico tornaria possível a miniaturização dessas armas. Pequenas organizações poderiam, algum dia, terem acesso a elas. Tal possível proliferação é atualmente considerada uma maldição, e não uma bênção. Por quê? Principalmente porque todos temem que tal proliferação de armas de destruição em massa, combinada com meios avançados para a entrega destas, intensifica “o problema da garantia da segurança global”, tal como Dagobert Brito e Michael Intriligator[1] recentemente escreveram em Economic Affairs.
A afirmação de que a proliferação de quaisquer armas — de pequeno ou grande porte, nas mãos de cidadãos comuns ou de políticos — é uma ameaça geral é, com efeito, o primeiro passo em direção a centralização e monopolização do poder. É a partir do argumento de que a própria proliferação é perigosa que, indivíduos ao redor do mundo, sendo proibidos de terem as armas por eles escolhidas, são privados do direito básico de se defenderem por (e de) tiranos governando seus próprios países.
Parte do problema é o medo instigado nos outros quando se possui armas. Imagine uma situação na qual armas nucleares em miniatura com grande poder de destruição estão disponíveis e acessíveis a cidadãos comuns. Eu poderia lançar um ultimato ao Governo Francês, tal como eles eventualmente fazem com outros governos. Meu ultimato seria, “caso vocês tomem meus recursos através de taxação e invasão de minha propriedade, eu destruirei Paris.” Ou pior, “Os residentes de Paris deverão me pagar um tributo ou serão aniquilados.”[2]
Fatos e o senso comum contrariam esse argumento simplista, na França, em 1991, houveram 16.000 prisões por posse de armas ilegais, e apenas 1.600 homicídios. Apenas 45% foram cometidos com armas, armas de fogo ou armas brancas. A probabilidade do uso de armas restritas é bem baixa — por volta de 45%. Uma vez que prisões envolvem apenas uma fração de pessoas carregando ou possuindo armas legais ou ilegais, a probabilidade real de armas proibidas serem usadas é bem baixa. E, claro, a única época na história em que se usou armas nucleares foi quando os Estados Unidos podiam usá-las sem medo de retaliação.
Seria a Proliferação uma Maldição?[3]
Temos de estabelecer uma correlação entre a posse de armas e o número de assaltos. O armamento legal ou ilegal aumenta a probabilidade de agressão ou a diminui? A probabilidade da guerra nuclear aumentaria caso mais países desenvolvessem armas nucleares? Brito e Intriligator, através do teorema da cardinalidade, tentaram mostrar tal correlação.[4] A tese deles era tradicional, na qual o fator dominante não era a proliferação das armas nucleares per se, mas o aumento de acidentes ou lançamentos inadvertidos pelos que as possuem. Alternativamente, o caso da não proliferação frequentemente foca na irracionalidade do ator marginal que pode destruir o “equilíbrio de terror das armas nucleares” — um clássico argumento usado para justificar um cartel.
Imaginemos que há somente uma pessoa armada. A tentação de ter uma conduta mais agressiva para a resolução de conflitos ao invés de uma conduta mais passiva seria fortíssima — pois ele tem uma vantagem comparativa. Agora, imaginemos duas pessoas (ou Estados) similarmente armadas. A questão fundamental é a de quem usará uma estratégia agressiva (Falcão), ou cooperativa (Pombo) em um conflito. Se o uso de armas levará a uma guerra mortífera na qual ambos os lados perderão não apenas suas propriedades, mas também suas vidas, uma estratégia agressiva não é a mais preferível. Se supormos que tanto um quanto o outro são entidades racionais, eles preferirão adotar o comportamento Pombo ao invés do comportamento Falcão apenas se o primeiro oferecer mais vantagens que o segundo. A complicação é que os ganhos futuros de cada uma das pessoas dependem do comportamento da outra. Também há uma probabilidade diferente de zero de conflito armado, embora essa possibilidade seja muito menor do que a no caso em que um grupo não corra risco de retaliação. Nesse caso, a estratégia falcão seria mais tentadora para o jogador armado.
Formalizemos,[5] então, essa interação entre John e Peter, dois indivíduos, ou príncipes representando seus países, ambos tendo armas nucleares:
| Peter | |||||
| 1–λ(2) | λ(2) | ||||
| John | Pombo | Falcão | |||
| Pombo | λ(1) | V/2 | V/2 | 0 | V |
| Falcão | 1–λ(1) | V | 0 | (–C) | (–C) |
V é a medida de ganho obtido de um conflito. C é o custo da guerra. Caso ambos se utilizem da estratégia Pombo, eles dividirão ganhos, V/2. Se houver equivalência nos níveis de poder, as armas nucleares fazem a guerra ser muito custosa. Quando ambos fazem guerra, o uso de armas nucleares só resulta em prejuízos, –C, para John e para Peter. Se for o caso em que John tem o monopólio de armas nucleares, ele não teme retaliação alguma; aqui, há apenas ganhos (V > 0) para John e nenhuma perdas ou ganho para Peter, já que ele se rende.
Se for o caso em que John tem o monopólio, a estratégia dominante para ele é a estratégia Falcão.[6] Se houver equivalência nos níveis de poder, cada jogador adotará a estratégia Falcão se e somente se houver certeza que o outro se utilizará da estratégia Pombo. Caso ambos se utilizarem da estratégia Falcão, resultará em puro prejuízo. E se John se utilizar da estratégia Falcão e Peter usar a estratégia Pombo, John terá a totalidade dos ganhos, V. Na situação oposta o ganho é zero. O jogo é simétrico desde que ambos os lados tenham as mesmas armas. Podemos ver que a estratégia Falcão não é o comportamento mais atrativo, visto que a consequência deste (–C) é negativa. Mas a estratégia Pombo é duvidosa, visto que V > V/2. Assim, John joga como Falcão apenas se Peter jogar como Pombo. Na ausência de uma previsão perfeita, John tem de prever o comportamento de Peter. Da perspectiva de John, λ(2) é a probabilidade de Peter adotar a estratégia Falcão, e 1–λ(2) é a de Peter adotar a estratégia Pombo. E, para Peter, λ(1) é a probabilidade de John adotar a estratégia Falcão e 1–λ(1) de adotar a estratégia Pombo.
Os ganhos futuros esperados para John caso adote a estratégia Falcão são:
(1) E(U)H = (1–λ(2))V + λ(2)(–C)
Caso ele jogue como Pombo os ganhos são:
(2) E(U)D = (1–λ(2))λV/2 + (2)λ0 = (1–λ(2))λV/2
Portanto, ele jogaria como Pombo se e somente se
(3) E(U)D = (1–λ(2))λV/2 > E(U)H = (1–λ (2))λV + λ(2)λ(–C)
e ele jogará como Falcão quando:
(4) E(U)D = (1–λ(2))λV/2 < E(U)H = (1–λ(2))λV + λ(2)λ(–C)
Ele será indiferente entre as duas estratégias quando:
(1–λ(2))λV + λ(2)(–C) = (1–λ(2))λV/2
Isto é, quando
(5) λ(2)* = V/(2C + V)
A interpretação da razão V/(2C + V) é, portanto, a relação entre os ganhos da estratégia Falcão, V, quando o outro jogar como Pombo; e os custos de oportunidade de guerra (2C + V),[7] quando o outro jogar como Falcão. Se John estimar que a probabilidade, λ(2), de Peter jogar como Pombo é menor que essa razão, λ(2)*, John jogará como Pombo. Do contrário, caso ele estime que essa probabilidade é maior que a razão, John jogará como Pombo. Também notamos que, conforme o aumento do dano resultado da guerra é comparado aos ganhos vindos desta, mais provável é que John (ou Peter) adote a estratégia Pombo, já que a probabilidade limite é menor. Caso a razão dos ganhos sobre os custos da guerra se aproxime de zero (que é o caso com as armas nucleares), a probabilidade de uma resolução pacífica de conflitos aumenta drasticamente. Agora, visto que o jogo está simétrico, temos λ(1)* = λ(2)*.
Em tal interação, λ(2) e λ(1) são variáveis chave na decisão de entrar em um conflito nuclear. Assumamos que John foi erroneamente convencido por um terceiro, Paul, que Peter jogará como Pombo, ou que há uma grande tendência de Peter jogar como Pombo (enquanto Peter na verdade está pronto para jogar como Falcão). Então John adotará a estratégia Falcão com base em uma informação incorreta. A guerra nuclear é, então, o resultado dessa informação incorreta. Isso explica o porquê de os governos terem desenvolvido comunicações diretas entre aqueles que têm poder para começar um conflito nuclear, protegendo-se contra tais informações errôneas. Mas como os jogadores são racionais, eles antecipam a dificuldade em prever o comportamento de outros. Um requisito de consistência natural é que as expectativas também são racionais.
A convergência de antecipações entre John e Peter é crucial. Considere a figura seguinte:
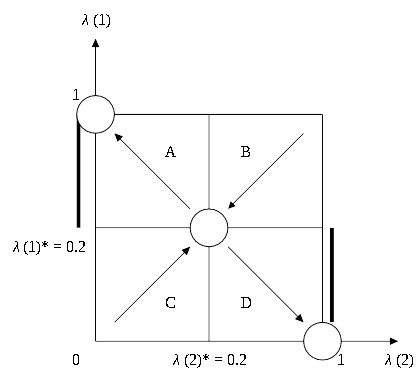
No eixo horizontal, delineamos as expectativas que John tem de Peter, λ(2), enquanto no eixo vertical nós delineamos as expectativas que Peter tem de John, λ(1). Assumamos que estamos na zona A. Nesse caso, λ(1) > λ(1)*, enquanto λ(2) < λ(2)*. Isso significa que Peter deveria jogar como Pombo, pois é a melhor resposta ao comportamento de John, já que John joga racionalmente como Falcão. Pois as expectativas na zona A, uma estratégia estável seria o par λ(1) = 1, λ(2) = 0. John joga como Falcão e Peter como Pombo. Na zona D, temos o oposto, λ(1) = 0, λ(2) = 1; John joga como Pombo e Peter joga como Falcão. Há puramente duas estratégias: Ou John domina ou Peter domina. Nas regiões B e C, tanto Peter como John jogam com a mesma estratégia, ambos Falcão ou ambos Pombo, já que λ(1) > λ(1)* e λ(2) < V(2)* (Zona B) λ(1) < λ(1)* e λ(2) < λ(2)*. O equilíbrio misto λ(1)* = λ(2)* não é de fato estável nas regiões A e D. Mas quando C aumenta drasticamente, como acontece com as armas nucleares, o valor de λ(1)* = λ(2)* = V/(2C+V) se aproxima de zero, de tal modo que as regiões de paz (A, B e D) crescem em tamanho. Isso demonstra um aumento na probabilidade de o resultado dessa interação ser a paz.
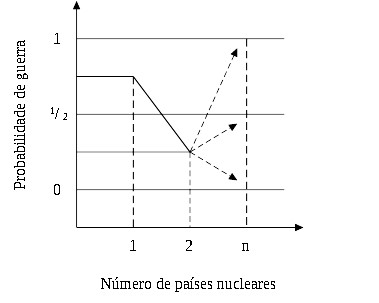
Consequentemente, a corrida armamentista entre dois países nucleares para estabelecer um equilíbrio de poder diminuiria a probabilidade de um conflito armado. Quanto mais mortal as armas se tornam, mais dissuasivas elas se tornam. A próxima questão é: A entrada de participantes adicionais aumentaria, diminuiria, ou deixaria inalterada a probabilidade de conflito? Consulte a próxima figura.
No eixo vertical está a probabilidade de guerra, e no eixo horizontal está o número de países ou governos com armas nucleares. Com um monopólio, a probabilidade da guerra se aproxima de 1. Com dois jogadores com arma nuclear, a probabilidade é próxima de zero. Ao adicionar participantes, ou essa probabilidade é abaixada para zero ou é aumentada até chegarmos a uma pura incerteza[8] (a probabilidade da guerra é 50) ou a pura certeza (a probabilidade de guerra se aproxima de 1).
Adicionar um jogador a interação implica em um novo jogo com três jogadores, cada um tendo sempre duas estratégias para jogar, Falcão ou Pombo:
| Patrick | Falcão (λ(2)) | Pombo (1–λ(2)) | ||
| Peter | Falcão (λ(3)) | Pombo (1–λ(3)) | Falcão (λ(3)) | Pombo (1–λ(3)) |
| John | ||||
| Falcão λ(1) | –C,–C,–C | –C,–C,–C | –C,–C,–C | V,0,0 |
| Pombo 1–λ(1) | –C,–C,–C | 0,V,0 | 0,0,V | V/3,V/3,V/3 |
Patrick joga de Falcão ou Pombo. Então Peter joga ou de Falcão ou de Pombo condicionado pelo fato de Patrick ter jogado como Falcão ou Pombo. Qual será a estratégia de John? Em um conflito nuclear, caso dois jogadores joguem como Falcão, o poder destrutivo das armas nucleares será tanto que o outro jogador que jogue de Pombo pode ser destruído também.[9] Com efeito, haverá ganhos para um ou para todos caso apenas um jogador jogue de Falcão enquanto os outros joguem de Pombo ou quando todos jogarem como Pombo.
Consequentemente, sabendo dessa matriz, John calculará o valor esperado em adotar a estratégia Falcão em contrapartida a estratégia Pombo, antecipando o comportamento agressivo dos outros jogadores.
Estratégia Falcão:
(6) E(U)H = λ(2)λ(3)(–C) + λ(2)(1–λ(3))(–C) + (1–λ(2))(1–λ(3))λV
Estratégia Pombo:
(7) E(U)D = λ(2)λ(3)(–C) + (1–λ(2))(1–λ(3))(V/3)
John jogará como Falcão quando:
(8) E(U)H = λ(2)λ(3)(–C)+λ(2)(1–λ(3))(–C)+ (1–λ(2))(1–λ(3))λV > E(U)D = λ(2)λ(3)(–C) + (1–λ(2))(1–λ(3))(V/3)
Ele será indiferente quando:
(9) E(U)H = λ(2)λ(3)(–C) + λ(2)(1–λ(3))(–C) + (1–λ(2)) (1–λ(3))λV =E(U)D = λ(2)λ(3)(–C) + (1–λ(2))(1–λ(3))(V/3)
Já que o jogo é simétrico, e, sabendo que as expectativas são racionais (isto é, as expectativas que cada jogador tem sobre o outro coincidem com as reais intenções de ação que os outros têm), podemos escrever: λ(1) = λ(2) = λ(3) = 3λ, onde 3λ é o limite de três jogadores. Ao resolver a equação 9 por 3λ, obtemos:
(10) 3λ = V/(3C + V)
O limite no qual John baseia sua estratégia é menor com três jogadores do que com dois jogadores. Adicionar um número N de jogadores neste jogo leva a um limite no qual todos os jogadores baseiam sua estratégia:
(11) Nλ = V/(NC + V)
Acrescentar N ao infinito reduz o limite para zero. Cada potência nuclear será incitada a jogar de Pombo. Adicionar N jogadores implica em N estratégias onde um jogador domina (isto é, joga como Falcão enquanto todos os outros jogam como Pombo) e um equilíbrio misto λ(1)* = … = λ(N)* = V/(NC+V). No espaço N-dimensional da λ(i), a área que correspondente a C no espaço bidimensional diminui para zero, garantindo alta estabilidade e paz.[10]
Para alguém que observa de fora, a frequência com a qual um conflito nuclear pode emergir é dada por
(12) f(H) = ∑N(i=1)Nλ +Π(Nλ)N
Olhando para a matriz com três jogadores, vemos que há três casos com dois jogadores em guerra, e um caso em que todos os jogadores estão em guerra. Mas o produto de uma probabilidade elevada à potência N é negligenciável. Assim, a frequência de uma guerra nuclear em uma matriz N de jogadores é reduzida a:
(13) f(H) = NV/(NC+V) = (V/C)/(1 + V/NC)
Conforme N se aproxima de infinito, a frequência de guerras nucleares é a razão dos ganhos V sobre os custos de guerra C. Com armas nucleares, C é muito maior que V, o que prediz que a frequência de guerras nucleares se aproximará de zero. A lição desta análise formal é a de que, quanto mais os jogadores estão armados, mais a probabilidade limite de haver conflitos armados dependerá da razão V/C. Quanto mais dissuasivos são os meios, menores são as chances de conflito. A formalização pode sempre ser suspeita de jogos retóricos, e esta não é uma exceção. Ao menos o modelo formal apela para a razão e não para a paixão. Se for o caso de que o modelo esteja correto, então é importante que se liberalize o direito de possuir armas extremamente perigosas e também que se aceite sua disseminação entre as nações ou indivíduos.
Seria a Proliferação Nuclear uma Bênção?
Sim, é uma bênção. Por quê? Porque o que é bom para nós também é bom para os outros. O equilíbrio do terror foi um assegurador da paz na Europa durante a guerra fria. Se não fosse por isso, os soviéticos poderiam ter tentado invadir a Europa. Quando não há armas nucleares, há guerras aos moldes clássicos. Que podem resultar em massacres comparáveis àqueles vistos com o uso de armas convencionais nas guerras mundiais. A guerra do Irã/Iraque é um caso pontual: se ambos os lados tivessem armas nucleares, eles poderiam ter hesitado entrar no conflito, salvando milhares de vidas.
Este tipo de suporte à proliferação de armas nucleares é natural para economistas, mas herético para não-economistas. Os países que são membros de uma associação nuclear formam um cartel que visa proteger seu monopólio em relação aos outros países. Até mesmo se utilizam de violência para prevenir que países que eles não gostam obtenham tecnologia nuclear. Se as armas nucleares reduzem a possibilidade de conflitos armados, isto é, protegem vidas humanas e territórios de invasões externas e violência, quer dizer que a possessão de armas nucleares é eficiente.
A posses de armas nucleares se tornará mais necessária conforme os custos de tecnologia nuclear diminuem. A competição entre países para se defenderem contra agressores externos levará à proliferação de armas nucleares. O cartel dos membros do clube nuclear (Rússia, Inglaterra, França, China e os Estados Unidos), falharão na medida em que mais países desenvolvam armas. Há duas grandes potências neste processo. Os membros do clube têm razões para trapacear e conceder armas nucleares a outros países (e.g. França, Iraque, China e Irã); e outros países podem entrar no mercado sem precisar de ajuda (e.g. Índia, Paquistão, Israel, Irã, Iraque, Coreia do Norte). Lembremos também que Cazaquistão, Belarus e a Ucrânia herdaram armas nucleares da URSS. Talvez se a Ucrânia manter seu arsenal nuclear, a Polônia decidirá adquirir armas nucleares, África do Sul, Japão, Alemanha, Brasil e Argentina terão armas, num futuro próximo, caso já não tenham.
Esse ponto de vista é compartilhado de forma crescente pelos estrategistas militares do Ocidente, muitos dos quais acreditam que países desejando obter tais armas deveriam ser ajudados, e não tratados como ilegais. Um artigo de J. Fitchett no International Herald Tribune[11] nota essa mudança de opinião entre oficiais militares. Mas Fitchett afirma que, caso a proliferação prevaleça, o risco de conflito aumenta devido a inabilidade de controlar o poder de dissuasão de todos. Especialistas do Pentágono notaram que, quando a comunicação entre a URSS e os Estados Unidos ficou limitada, houve minimização do comportamento provocativo. Fitchett continua: com territórios como a Ásia e o Oriente Médio, a paixão nacionalista e o comportamento irracional são realidades. Estes líderes são frequentemente autocráticos e estão prontos para destruir seus países em um conflito nuclear apenas para satisfazer seus interesses ou apetites territoriais. Até mesmo o conflito no Iraque em 1991 mostrou o oposto (Saddam Hussein sequer se atreveu a usar armas químicas sob ameaça nuclear de Israel e dos Estados Unidos), não podemos extrapolar isso para um mundo onde armas nucleares são um papel banal. Não devemos nos esquecer que um conflito nuclear não é um conflito local e pode afetar, tal como aconteceu com o desastre de Chernobyl, terceiros que sequer estavam envolvidos. Este argumento não é novo — é similar a um dos argumentos utilizado por médicos e farmacêuticos franceses, que, sob a bandeira da proteção ao consumidor, impedem a venda de medicamentos em supermercados. Um outro argumento afirma que a competição em serviços de linhas aéreas leva a um aumento dos acidentes devido às empresas aéreas não investirem o suficiente em segurança sob a pressão de competição. Isto foi provado como sendo falso. Todos os defensores de monopólio e cartéis usam argumentos parecidos, incluindo argumentos a respeito das armas nucleares.
É difícil acreditar que um monopólio de motoristas de táxi protegeria o consumidor. Mas quando uma junta médica anuncia que um monopólio beneficia o consumidor, o público é persuadido. Obviamente, o raciocínio é distorcido quando os argumentos se relacionam com nossas vidas. Dessa maneira, quando pensamos em armas nucleares, frequentemente perdemos a habilidade de pensar de forma clara.
Retornemos ao argumento econômico. Antes de 1989 havia uma paridade nuclear entre os Estados Unidos e a URSS. Podemos considerar essa situação como uma bipolaridade de Cournot. A questão central daquela época era a corrida em direção ao armamento nuclear. Para um dado nível de armamento soviético, igualá-lo a produção de mísseis dos Estados Unidos era lucrativo, conforme a capacidade de dissuasão. Do mesmo modo, para um dado nível de capacidade ofensiva americana, era vantajoso igualá-lo às ogivas nucleares soviéticas.
A interseção entre estas duas funções é o equilíbrio de Cournot. O número de mísseis sendo produzidos era muito alto. Era possível aperfeiçoar os resultados para ambos os adversários através de uma redução mútua de produção de armamentos. Se ambas as partes concordam em reduzir seus exércitos enquanto retém a capacidade de dissuasão, seria ótimo para eles não perderem essa oportunidade. No começo da Guerra Fria nós testemunhamos conferências para redução dos exércitos e tratados de não-proliferação. Cada um dos lados nesses acordos teria mantido uma certa cota de produções de mísseis ou comprariam estoques até um nível que maximizasse o lucro para ambas as partes.
Todas essas conferências entre superpotências foram simples acordos para otimizar a troca entre custos e dissuasão. A falha de tais acordos é intrigante. Por que falharam? Pois os acordos têm de ser respeitados. A maioria desses tratados não apenas deram detalhes exatos a respeito no que diz respeito a cotas de produção, mas também sobre os meios de verificar se as cotas foram ou não respeitadas. Em outras palavras, o problema do acordo em um cartel criou o dilema do prisioneiro. Tinha vantagem o que trapaceasse em vez do que respeitasse o acordo. Este incentivo a não respeitar as regras do acordo explica a falha dos tratados. A Guerra Fria foi caracterizada pela produção de mísseis até o ponto de Cournot, com tentativas de reduzir estes exércitos no ponto de equilíbrio. Apenas com o fim da União Soviética que essa estratégia de interdependência acabou — a estrutura bipolar desapareceu
Duas Vias para o Desenvolvimento Futuro
Os Estados Unidos têm um monopólio na dissuasão nuclear e desempenham o papel de um poder executivo mundial, impedindo trocas internacionais para países que buscam por armas nucleares. Essa é uma posição custosa, e os Estados Unidos não possuem reivindicações legítimas para desempenhar tal papel.
Deveríamos permitir que mais e mais países desenvolvam armas nucleares.
A primeira lição da história é que, na ausência de um monopólio coercitivo, nenhum acordo ou cartel, até mesmo um organizado por Estados, pode sobreviver. Um dos melhores exemplos disso foi o cartel do petróleo. A segunda lição é a de que a competição é o meio pelo qual maximizamos os nossos lucros decorrentes de uma troca. A posse de armas nucleares é a forma mais eficiente de defender um território, pois elas produzem medo. Isso reduz a quantidade de conflitos armados e não requer muitas pessoas. Tal tecnologia, conforme vai se tornando mais acessível, enfrentará uma demanda crescente vinda de países com menos recursos. Tal democratização é o resultado de uma competição.
Uso o termo “democratização” em vez de “disseminação” para fazer um ponto. Para muitos, “democratização” tem uma conotação positiva. Caso um pobre iraquiano ou polonês possa se beneficiar de tal proteção, é “democratização”. Para um francês ou americano rico, é “disseminação”. Para um economista, competição.
O argumento de que um iraquiano, polonês, ou líbio é mais irracional que um francês é fundamental. Este é o argumento usado contra a proliferação de armas nucleares. Foi evocada durante a Guerra do Golfo. Saddam Hussein não é um de nós, ele não compartilha valores conosco e, ainda, ele é um ditador sanguinário, mas ele não é irracional ou louco. Mas aqueles que compartilham desse ponto de vista insistem em dizer que não podemos extrapolar do caso de Saddam Hussein. Mesmo assim, se seguirmos essa lógica, teremos de demonstrar que sistemas políticos não-democráticos constantemente são liderados por pessoas loucas e irracionais. Não há como provar isso. Seria também necessário provar que sistemas políticos democráticos estão imunes a tal fenômeno. Hitler e os nacional-socialistas vieram ao poder através de mecanismos democráticos. Assim, esse argumento também falha.
Podemos conectar essa teoria àquela que proíbe cidadãos de terem armas de fogo. O problema com essa proibição é que os cidadãos ficam indefesos e as únicas pessoas armadas são a polícia, que frequentemente não sabem como atirar, ou miram suas armas contra civis inocentes; ou gangsters, que usam suas armas contra cidadãos, estes que foram desarmados pelo Estado. Também notamos que, dentro de qualquer território dado, uma legislação flexível acerca do armamento civil leva a uma diminuição do crime. Os mecanismos propostos para cuidar dessa tendência, mostrados de forma mais notável por John Lott,[12] são as mesmas que eu digo que diminuirão conflitos multinacionais seguidos pela proliferação livre de armas nucleares.
Gostou do artigo? Leia o livro de Hans Hermann Hoppe chamado Mito da Defesa Nacional
Quer saber mais sobre o autor?
Acesse agora sua wiki.
Faça parte do clube da liberdade.
Inscreva-se em nosso Canal Universidade Libertária no Youtube
Notas de Rodapé
[1] D. Brito e M. Intriligator, “Deterring nuclear weapons proliferation”, em Defence Economics, Economic Affairs IEA (Dezembro de 1977).
[2] Com efeito, no presente, apenas os governos, e através de taxação massiva, são capazes de financiar armas nucleares.
[3] Aqui, estou em dívida com Nikolay Gertchev, que me ajudou a desenvolver um modelo formal de conflito baseado na interação tradicional Falcão e Pombo na teoria dos jogos.
[4] D. Brito e M. Intriligator, “Proliferation and the Probability of War”, Journal of Conflict Resolution (Março 1996): 206-14.
[5] Este modelo é uma variante do modelo Falcão e Pombo da teoria dos jogos moderna, desenvolvido inicialmente por J.M. Smith, Evolution and the Theory of Games (Cambridge, Reino Unido: Cambridge University Press, 1982).
[6] Assimetrias, desequilíbrio de poder e hierarquia de forças políticas são geralmente as fontes de poder político. Na análise, assumimos uma simetria perfeita de forças como resultado da disseminação das armas nucleares: a tecnologia militar está disponível ou acessível a um determinado preço para indivíduos ou grupos. Vamos abandonar essa hipótese. Introduzimos assimetria entre John e Peter. Os custos e ganhos para eles são divergentes. A matriz é a seguinte:
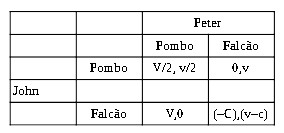
Damos a Peter uma vantagem na agressão, v – c > 0. John está ciente de que Peter jogará contra Hawk devido a esta vantagem. Porque Peter definitivamente jogará Hawk, a estratégia de John será se render a Peter, uma vez que 0 > –C. Peter vence John. Essa interação levará à dominação de um partido, que estranhamente é elogiado por cientistas políticos. A origem de tal dominação não está necessariamente na assimetria em si, mas na crença nela por parte de John. Isso ajuda a destacar o papel da desinformação como estratégia militar, bem como o papel da tecnologia em conflitos multinacionais.
[7] 2C + V mede para ambos os jogadores a soma do custo direto da guerra, C, e a perda sofrida por cada jogador ao perder o ganho da estratégia Pombo, V/2. 2(C + V / 2) = 2C + V.
[8] Brito e Intriligator reconhecem os casos de monopólio e duopólio, mas argumentam que um aumento no número de jogadores aumentará a probabilidade de erros. Nesse caso, a probabilidade de conflito aumenta para 0,50 — isto é, para completar a incerteza.
[9] Um pensamento é que o terceiro que não participar do conflito nuclear será o último sobrevivente e lucrará com a destruição de seus concorrentes na luta por recursos. Na verdade, esta estratégia move o terceiro jogador para a autarquia, o que implica em perdas em relação à situação atual de nenhum conflito. Além disso, podemos acrescentar um problema de externalidade — dano colateral — com a guerra nuclear devido ao poder destrutivo das armas nucleares.
[10] A ideia subjacente é simples: se k jogadores antecipam que N–k jogadores vão jogar de Pombo, λi <λ (i)*, assim, a melhor estratégia é jogar de Falcão. Mas se todos eles jogarem Falcão ao mesmo tempo, o resultado será um conflito generalizado e seu próprio desaparecimento devido às externalidades de um conflito nuclear. Sabendo que cada um dos k jogadores prevê que os k–1 outros jogadores terão a mesma aposta, eles jogarão de Falcão apenas se tiverem certeza de que todos os outros jogarão de Pombo. Essa possibilidade diminui drasticamente na medida em que o número de jogadores aumenta.
[11] International Herald Tribune, http://www.iht.com/diplo.
[12] John R. Lott, Jr., More Guns, Less Crime: Understanding Crime and Gun Control Laws (Chicago: University of Chicago Press, 1998).

